QW unit creator¶
Quantum wells have been developed in the context of solar cells mainly to tailor the absorption edge of the sub-cells in multi-junction devices to their optimum values ([4]). Typically, achieving the proper performance requires a delicate trade-off between carrier collection and light absorption ([5], [6]). Solcore includes a simplified QW structure in the PDD solver in order to calculate the performance of solar cells containing them. Contrary to other programs like Nextnano, Solcore does not solve the Schrödinger equation and the PDD equations self-consistently: first, the energy levels of the quantum wells are solved using a flat-band condition, considering also the strain in the materials, and then an effective band structure is used to solve the transport equations in a bulk-like fashion. This is illustrated in the next figure:
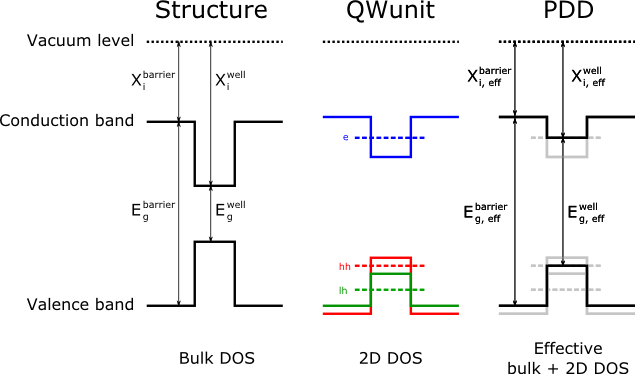
From the perspective of the PDD solver, the actual bandgap and electron affinity of each layer in a quantum well depend on the energy levels, i.e. the minimum energy for electrons is not the band edge of the conduction band, but the ground confined level. The same applies to holes, with the actual band edge being the maximum between the ground states of light holes and heavy holes. The resulting band profiles used in the PDD solver are shown in the right end of the figure.
To use QWs in the PDD solver, we create an effective electron affinity and bandgaps for all layers in the QW. For the barriers, the electron affinity and band gap are the same as they are in bulk, modified by the strain, if necessary. For interlayers, if present, it depends on what is higher, the band edges of the interlayer or the confined carrier levels.
The density of states and the absorption profile need to be modified in a similar way. For the density of states:
- Barriers have the bulk density of states and absorption profile.
- Interlayers only have the bulk density of states above the barrier and the bulk absorption from the barrier energy and zero below that.
- Wells have all the density of states associated with the confined states and the bulk density of states above the barrier, while they have the absorption of the confined levels below the barrier energy and of the bulk above it.
These simplifications are similar to those in Nelson et al. ([2]) and in Cabrera et al. ([3]) and allow us to keep the bulk-like form of the carrier densities in the drift diffusion equations under the Boltzmann approximation. A more rigorous treatment will be necessary in the presence of tunnel transport across a supperlattice, tunnel escape from the QWs to the barriers - possible in the presence of high electric fields - and in the case of very deep QWs, when carrier escape from the less confined levels might be possible but not from the deeper ones. In these situations, a set of rate equations linking the different levels, as well as a self-consistent solution of the transport and Schrödinger equations would be required, besides using more advanced methods such as a non-equilibrium Green’s functions (NEGF) formalism ([7]).
The QWunit class¶
This module defines a class derived from solcore.Structure that allows to solve the Schrodinger equation and the kp model. It also prepares the properties of the structure (bandedges, efective density of states (DOS), etc) in order to have a meaningful set of properties for the PDD. Without this preparation, the structure is just a collection of layers with bulk-like properties, as it is illustrated in the figure:
-
class
QWunit(*args, **kwargs)¶ Asembles a group of layers as a quantum well, calculating its properties as a whole. As with any solcore.Structure, a QWunit usually gets as input a list of solcore.Layers and a solcore.material as substrate (defined with the keyword ‘substrate’). In this case, the class constructor is designed to work specifically for the PDD solver so it requires the following:
- It needs a minimum of 3 layers.
- There must be exactly one layer with the role = “well”.
- Top and bottom layers are assumed to be the barriers.
- Anything not a barrier nor a well will be considered as “interlayer”.
- A substrate.
Since the PDD solver can not work with superlattices, there is no point of considering the solution of more than one QW. All QWs entering into the solver are independent, regardless of the width of the barriers. To account for the possible presence of nearby QWs, perdiodic boundary conditions can be used to solve the Schrodinger equation. If barriers + interlayers are thick enought, this make no difference but if they are thin, it affects the number and energy of the confined levels. It does not ‘create’ minibands, though, so the results with thin barriers must be used with caution.
-
solve([V=0, WLsteps=(300e-9, 1100e-9, 201), wavelengths=None, periodic=True, filter_strength=0.0, blur=None, blurmode="left", offset=0, use_kp=True, use_Adachi=False, calculate_absorption=True, alpha_params=None, T=293])¶ Solves the structure, calculating the energy levels, the absorption, etc. First, it calls the Schrodinger solver and then it uses the result to obtain an effective band profile for the conduction and valence band, an effective density of states considering both, the bulk and quantum levels, and the absorption coefficient. This is done for each layer of the structure (see the following methods for details). The input parameters of this method are the same that for the Schrodinger solver except for the wavelengths definition that can be used as default (WLsteps) or be added with ‘wavelengths’.
The method returns as output the output dictionary of the Schrodinger solver.
-
RecalculateBandEdges(use_kp, SR)¶ From the perspective of the PDD solver, the actual bandgap and electron affinity of each layer depend on the energy levels, i.e. the minimum energy for electrons is not the band edge of the conduction band, but the ground confined level. The same applies to holes, being the actual band edge the maximum between the ground states of light holes and heavy holes (see figure-QWunit).
In this method we modify that by creating an effective electron affinity and band gaps for all layers in the QW. For the barriers, the electron affinity and band gap are the same than in bulk, modified by the kp calculation, if necessary. For interlayers, it depends on what is higher, the bandedges of the interlayer or the confined carrier levels.
It requires as input if kp should be used to recalculate the band positions and effective masses (‘use_kp=True’) and the output of the Schrodinger solver.
-
RecalculateDensityOfStates(SR)¶ Calculates the effective density of states for each layer in the QW. The general rule is: - Barriers have the bulk density of states - QW have ALL the density of states asociated with the confined states + bulk density of states above the barrier - Interlayers have only the bulk density of states above the barrier
This simplification is similar to that in Nelson et al. [2] and allow us to keep the bulk-like form of the carrier densities in the drift diffusion equations under the Boltzmann approximation. From a physical porint of view, it probably can be done better.
-
CalculateAbsorption(use_Adachi, SR): If required, this function calculates the absorption of the QW, putting together the absorption of the confined levels and the absorption of the bulk. As with the density of states, the rules are:
- Barriers have the bulk absorption
- Interlayers have the bulk absorption from the barrier energy and zero below that
- Wells have the absorption of the confined levels below the barrier energy and of the bulk above it.
The calculation is similar to that in [3] but, as with the DOS, it can probably be improved.
The required input is if Adachi method [1] for calculating the absorption should be used (‘use_Adachi=True’) and the output of the Schrodinger solver.
-
GetEffectiveQW(calculate_absorption=True, wavelengths=None, periodic=True, filter_strength=0.0, blur=None, blurmode="left", use_kp=True, use_Adachi=False, alpha_params=None)¶ Considers the device as a QW and solves its properties, including the modification of the bandeges due to strain, the efective mases and the absorption coefficient. Without calling this function, the structure is just a collection of layers with bulk-like properties.
Output: A list of layers with the effective properties of the QWs, repeated as many times as needed in case of a MQW.
# This example illustrates the creation of a QW structure with 40 wells, solve its quantum properties and # add it to the intrinsic region of a p-i-n solar cell import solcore.poisson_drift_diffusion as PDD from solcore.structure import Layer from solcore import material # First, we create the materials of the QW QWmat = material('InGaAs') (T=300, In=0.2) Bmat = material('GaAsP') (T=300, P=0.1) i_GaAs = material('GaAs') (T=300) # The QW is 7 nm wide, with GaAs interlayers 2 nm thick at each side and GaAsP barriers 10 nm thick. # The final device will have 40 of these QWs. QW = PDD.QWunit( [Layer(width = 10e-9, material = Bmat, role="barrier"), Layer(width = 2e-9, material = i_GaAs, role="interlayer"), Layer(width = 7e-9, material = QWmat, role="well"), Layer(width = 2e-9, material = i_GaAs, role="interlayer"), Layer(width = 10e-9, material = Bmat, role="barrier") ], T = 300, repeat = 40) # We solve the quantum properties of the QW effective_QW = QW.GetEffectiveQW(QW)
In this case, “effective_QW” is a list of 200 layers (5 layers per QW unit repeated 40 times) but rather than the bulk material properties, they include effective properties as a result of the quantum calculation.
All functions description¶
-
class
solcore.poisson_drift_diffusion.QWunit.QWunit(*args, **kwargs)[source]¶ Assembles a group of layers as a quantum well, calculating its properties as a whole
- It needs a minimum of 3 layers
- There must be exactly one layer with the role = “well”.
- Top and bottom layers are assumed to be the barriers.
- Anything not a barrier not a well will be considered as “interlayer”.
Since the Poisson - Drift-Diffusion solver can not work with superlattices, there is no point of considering the solution of more than one QW. All QWs entering into the solver are independent, regardless of the width of the barriers.
To account for the possible presence of nearby QWs, perdiodic boundary conditions can be used to solve the Schrodinger equation. If barriers + interlayers are thick enought, this make no difference but if they are thin, it affects the number of confined levels. It does not ‘create’ minibands, though, so the results with thin barriers must be used with caution.
-
RecalculateKP(index, mode)[source]¶ Recalculates the band structure of the QW unit to account for modifications due to strain.
This is already done in the Schrodinger solver, but it does not produce that information as output. We do it so here.
-
get_average_params(x, y)[source]¶ Calculates the average value of a parameter y in each layer of the structure.
Parameters: - x – x values
- y – the parameter of interest at positions x
Returns: the average value of y in layer i
-
get_probability_per_layer(x, y)[source]¶ Calculates the average value of a parameter y in each layer of the structure.
Parameters: - x – x values
- y – the parameter of interest at positions x
Returns: the average value of y in layer i
-
RecalculateBandEdges(mode, SR)[source]¶ The effective bandgap and effective affinity of each layer depends on the energy level, e.g.: the minimum energy for electrons is not the band edge of the conduction band, but the ground level. In this function we modify that creating an effective electron afinity and band gaps for all layers in the QW.
For the barriers, the electron afinity and band gap is the same than in bulk, modified by the kp calculation, if necesary.
-
RecalculateDensityOfStates(SR)[source]¶ Calculates the effective density of states for each layer in the QW. The general rule is:
- Barriers have the bulk density of states
- QW have ALL the density of states asociated with the confined states + bulk density of states above the barrier
- Interlayers have only the bulk density of states above the barrier
This simplification is similar to that in J. Nelson, M. Paxman, K. W. J. Barnham, J. S. Roberts, and C. Button, “Steady-state carrier escape from single quantum wells,” IEEE J. Quantum Electron., vol. 29, no. 6, pp. 1460–1468, 1993.
From a physical porint of view, it can certainly be done much better
-
CalculateAbsorption(use_Adachi, SR)[source]¶ If required, this function calculates the absorption of the QW, putting together the absorption of the confined levels and the absorption of the bulk. As with the density of states, the rules are:
- Barriers have the bulk absorption
- Interlayers have the bulk absorption from the barrier energy and zero below that
- Wells have the absorption of the confined levels below the barrier energy and of the bulk above it. The calculation is similar to: C. I. Cabrera, J. C. Rimada, J. P. Connolly, and L. Hernandez, “Modelling of GaAsP/InGaAs/GaAs strain-balanced multiple-quantum well solar cells,” J. Appl. Phys., vol. 113, no. 2, p. 024512, Jan. 2013.
-
solve(Efield=0, WLsteps=(3e-07, 1.1e-06, 801), wavelengths=None, periodic=True, filter_strength=0.0, blur=None, blurmode='left', offset=0, mode='kp8x8_bulk', use_Adachi=False, calculate_absorption=True, alpha_params=None, T=293)[source]¶ Solves the structure, calculating the energy levels, the absorption, etc.
-
GetEffectiveQW(calculate_absorption=True, wavelengths=None, periodic=True, filter_strength=0.0, blur=None, blurmode='left', mode='kp8x8_bulk', use_Adachi=False, alpha_params=None)[source]¶ Considers the device as a QW and solves its properties, including the modification of the bandeges due to strain, the efective mases and the absorption coefficient. The output is a list of layers made with materials with the effective properties after considering all these effects in addition to the quantum confinement.
Parameters: - device – The device structure
- calculate_absorption – If absorption must be calculated
- WLsteps – wavelengths in which to calculate the absorption (input for np.linspace function)
- wavelengths – An array with the waveengths
- periodic – If it has to be assumed that the structure is perdiodic
- filter_strength –
- blur –
- blurmode –
- mode –
- use_Adachi –
- alpha_params –
Returns: A dictionary with the output of the Schrodinger solver.
References¶
| [1] |
|
| [2] | (1, 2)
|
| [3] | (1, 2)
|
| [4] | Thomas, T., Wilson, T., Führer, M., Alonso-Álvarez, D., Ekins- Daukes, N.J., Lackner, D., Kailuweit, P., Philipps, S.P., Bett, A.W., Toprasertpong, K., Sugiyama, M., Okada, Y.: Potential for reaching 50% power conversion efficiency using quantum heterostructures. In: 6th World Conference on Photovoltaic Energy Conversion, pp. 1–2 (2014) |
| [5] | Alonso-Álvarez, D., Führer, M., Thomas, T., Ekins-Daukes, N.: Elements of modelling and design of multi-quantum well solar cells. In: 2014 IEEE 40th Photovoltaic Specialists Conference (PVSC), pp. 2865–2870 (2014) |
| [6] | Alonso-Álvarez, D., Ekins-Daukes, N.J.: Quantum wells for high- efficiency photovoltaics. In: Freundlich, A., Lombez, L., Sugiyama, M. (eds.) Physics, Simulation, and Photonic Engineering of Pho- tovoltaic Devices V, vol. 9743, p. 974311. SPIE OPTO, San Francisco, CA (2016). https://doi.org/10.1117/12.2217590 |
| [7] | Aeberhard, U.: Quantum-kinetic perspective on photovoltaic device operation in nanostructure-based solar cells. J. Mater. Res. 33, 373–386 (2018) |
