Rigorous Coupled Wave Analysis (S4)¶
Example 1: Comparing optical models (TMM, Beer-Lambert, and RCWA)
Solcore’s capacity for modelling periodic nanophotonic structures is provided through an interface with the 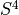 Python extension,
an implementation of RCWA (Rigorous Coupled Wave Analysis) developed in the Fan Group in the Stanford Electrical Engineering Department.
The documentation for S4 can be found here. The basic mechanics of the RCWA module are:
Python extension,
an implementation of RCWA (Rigorous Coupled Wave Analysis) developed in the Fan Group in the Stanford Electrical Engineering Department.
The documentation for S4 can be found here. The basic mechanics of the RCWA module are:
Solcore translates the relevant inputs (list) into the appropriate notation for
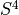
Solcore calls
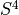 and feeds in the relevant inputs
and feeds in the relevant inputsSolcore translates the outputs from
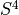 into the relevant outputs, which match the outputs from Solcore’s other optics methods (absorption, reflection, transmission, absorption profile with depth).
into the relevant outputs, which match the outputs from Solcore’s other optics methods (absorption, reflection, transmission, absorption profile with depth).
To use  from within Solcore, first make sure S4 is installed from the custom branch compatible with Python3.
from within Solcore, first make sure S4 is installed from the custom branch compatible with Python3.
Layers in the SolarCell object are defined in the usual Solcore way, but now have an additional geometry attribute, e.g.:
# define materials
Air = material('Air')(T=T)
TiO2 = material('TiO2', sopra=True)(T=T) # for the nanoparticles
# define a layer with circular discs
NP_layer = [Layer(si('50nm'), Air, geometry=[{'type': 'circle', 'mat': TiO2,
'center': (200, 200), 'radius': 50}])]
The geometry attribute is a list of dictionaries containing relevant entries. You can add more than one shape
per layer by simply adding more dictionaries to the list; each dictionary defines one shape, which is assumed to be periodic
in two directions. The necessary information to define shapes is:
For all shapes:
‘type’: ‘circle’, ‘ellipse’, ‘rectangle’ or ‘polygon’
‘mat’: the material the shape is made of; a Solcore material object.
‘center’: a tuple giving x and y coordinates (in nm) of the centre of the shape: (x, y)
Additional shape-dependent parameters:
Circle: * ‘radius’: a number in nm
Ellipse: * ‘angle’: a number in degrees, defining the angle by which the x-axis of the shape should be rotated (counter-clockwise). * ‘halfwidths’: a tuple of halfwidths in the x and y directions: (hw_x, hw_y)
Rectangle: ‘angle’ and ‘halfwidths’, as before
Polygon: * ‘angle’ as before * ‘vertices’: a tuple of tuples; each entry in the outer tuple are the x- and y-coordinates of the vertices of the (unrotated) polygon, one after another, in counter-clockwise order, e.g. ((x1, y1), (x2, y2), (x3, y3)). Coordinates are in nm.
Additionally, you should set the lattice vectors u and v defining the unit cell in your user options, and the number of Fourier orders to keep in the calculations in opts.orders:
opts.size = ((400, 0), (0, 400)) # lattice vectors for a square grating with period 400 nm
opts.size = ((400, 0), (400 / 2, np.sin(np.pi / 3) * 400))
# lattice vectors for a grating with hexagonal symmetry (triangular unit cell)
opts.orders = 19 # keep 19 Fourier orders
The calculation should converge for a higher number of orders, but computational time increases dramatically with the number of orders (scaled as the number of orders cubed).
Note that all dimensional information for the size and geometries should be in nm!
The RCWA interface for the solar cell solver¶
This is the method actually called from the solar cell solver, serving as interface between the solar cell and the RCWA formalism. The Beer-Lambert calculator, TMM calculator and the external optics calculator (where the user simply adds the reflection and the absorption profile manually) have similar interfaces.
The RCWA solver can handle different input angles and polarizations, specified in the options (specifically, options.theta, options.phi and options.pol). Theta is the polar angle while phi is the azimuthal angle clockwise from the y-axis. Both angles are in degrees, while pol is ‘s’, ‘p’ or ‘u’ (computationally, ‘u’ is simply the average of ‘s’ and ‘p’ and thus requires two calculations - therefore it will take twice as long.)